Números Egípcios
A calculadora exibe um número nos hieróglifos do Antigo Egito. Vários números são reconhecidos como fração Egípcia.
Esta calculadora exibe um número na forma de antigos hieróglifos Egípcios. O antigo sistema de numeração Egípcio foi usado desde cerca de 3000 a.C. por três a quatro mil anos. A descrição do sistema numérico pode ser encontrada logo abaixo da calculadora.
O antigo sistema de numeração Egípcio 1
Os antigos Egípcios desenvolveram o sistema de numeração baseado em 10, sem dúvida porque um ser humano possui dez dedos. Eles tinham os símbolos para representar unidades, dezenas, centenas, milhares, dezenas de milhares e milhões:
| Hieróglifo | Valor | Descrição |
|---|---|---|
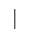 |
1 | golpe |
 |
10 | armadilha para gado |
 |
100 | bobina de corda |
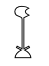 |
1 000 | planta de lótus |
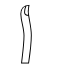 |
10 000 | dedo |
 |
100 000 | girino |
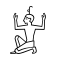 |
1 000 000 | deus Heh |
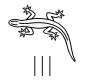 |
Muitos milhões (infinito) | lagarto com três golpes |
O símbolo correspondente é repetido para representar um número de 2 a 9, várias dezenas, várias centenas, etc.
Ordem de inscrição
Os antigos Egípcios esculpiam ou pintavam a maioria de seus hieróglifos da direita para a esquerda, mas às vezes a ordem de inscrição era invertida. Nossa calculadora produz a sequência de hieróglifos numéricos em ordem invertida com símbolos de grau superior à esquerda e símbolos de grau inferior à direita. Você pode reconhecer a ordem de leitura pelas figuras com rosto - comece a ler em direção à frente de sua cabeça.
Frações Egípcias
Os antigos egípcios escreviam um número fracionário pela soma de frações unitárias. Por exemplo, o número 0.89 (89/100) pode ser expandido para a soma das frações unitárias: 1/2+1/3+1/18+1/900. Leia Frações Egípcias para mais detalhes.
Um símbolo especial representado 1/2, e os outros denominadores de fração unitária foram inscritos sob o símbolo da boca.
| Hieróglifo | Descrição |
|---|---|
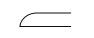 |
1/2 - metade |
 |
o símbolo da boca foi colocado sobre um denominador de fração unitária |
-
Donald Frazer, Hieróglifos e Aritmética dos antigos escribas Egípcios ↩
Comentários