Calculadora online: Volume de tanque cilíndrico inclinado

Para executar o cálculo, você deve fornecer o tamanho do tanque, ângulo de inclinação e nível do líquido.

Medição de nível do líquido

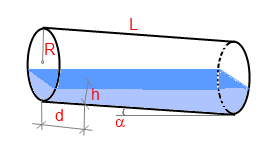
Você deve medir o nível do líquido na linha média do tanque perpendicular ao fundo do tanque. (Veja a imagem). Você pode medir o nível do líquido a qualquer distância de uma das bases (se fizer assim, deve inserir a distância em um parâmetro especial).
Alternativamente, você pode inclinar o tanque para atingir o nível de líquido zero na base superior; neste caso, você deve medir apenas o ângulo de inclinação.

Você pode encontrar detalhes de cálculos e fórmulas abaixo da calculadora.

Volume do líquido em tanque cilíndrico inclinado

Comprimento do cilindro

Raio do cilindro

Ângulo de inclinação (graus)

Nível do líquido

Nível próximo medido

base superior

base inferior

Distância da base

Distância entre o local de medição do nível de líquido e a base mais próxima. (0 se o nível for medido bem perto da base).

Precisão de cálculo

Dígitos após o ponto decimal: 2

Nível do líquido próximo à base superior

Nível do líquido próximo à base inferior

Comprimento da parte parcialmente preenchida do tanque

Comprimento da parte totalmente preenchida do tanque

Volume do líquido

Eu não consegui encontrar uma solução pronta para calcular o volume de líquido em um cilindro inclinado, então deduzi a fórmula desta maneira:

Fórmula de volume do tanque inclinado preenchido parcialmente

$V = \frac{R^2}{2}\int_{\small0}^L {\theta(x)-\sin{\theta(x)}dx$
onde $\theta(x)$ - como o ângulo do segmento depende do comprimento do cilindro x,
pode ser deduzido como
$\theta(x)=2\arccos{\frac{R-h}{R}}=2\arccos{\frac{R-(x\tan{\alpha}+h_{0})}{R}}$
onde
a - ângulo de inclinação,
h0 - nível de líquido na base superior

Se substituirmos essa expressão na fórmula, iremos obter:
$V = R^2\int_{\small0}^L {\arccos{u}-u\sqrt{1-u^2}dx=-\frac{R^3}{\tan{\alpha}}\int_{\small{u_0}}^{u_L} {\arccos{u}-u\sqrt{1-u^2}du$
onde $u=\frac{R-(x\tan{\alpha}+h_{0})}{R}$

Se tomarmos a integral, obteremos a seguinte solução:
$V = -\frac{R^3}{\tan{\alpha}}\left( u\arccos{u}-\frac{1}{3}\sqrt{1-u^2}(u^2+2)\right)\large|_{\small{u_0}}^{u_L}$
$= \frac{R^3}{\tan{\alpha}}\left( K\arccos{K}-\frac{1}{3}\sqrt{1-K^2}(K^2+2)-{C}\arccos{C}+\frac{1}{3}\sqrt{1-C^2}\left(C^2+2\right) \right)$

onde
$K=1-\frac{h_{0}}{R}$ ,
$C=K-\frac{{L}tan{\alpha}}{R}$

Determine o comprimento da parte do tanque preenchida com líquido

As fórmulas acima são usadas para o cálculo do volume do tanque inclinado com estes princípios:

Ambas as bases parcialmente preenchidas com líquido.
O nível do líquido h₀ é medido diretamente na base superior.
Nenhuma parte do tanque está seca ou totalmente preenchida.

Entretanto, a calculadora aceita o nível de líquido medido a alguma distância próximo à base superior ou inferior. Algumas partes do tanque podem estar secas ou totalmente preenchidas.

Para calcular o nível de líquido diretamente na base superior h_u utilize as fórmulas:
$h_u=h_{ll}-(L_c-l_l){\tan{\alpha}}$
onde h_ll - nível de líquido medido na distância l_l da base inferior, L_c - comprimento do tanque
$h_u=h_{lu}-l_u{\tan{\alpha}}$
onde h_lu - nível do líquido medido na distância l_u da base superior.
Se h_u for igual ou superior a zero, nós reconhecemos h₀=h_u, e L_f = L_c.

Parte vazia do tanque

Caso contrário, h_u pode ser negativo. Isso significa que alguma parte do tanque está vazia. Neste caso, assuma h₀=0 e calcule a parte L_f remanescente (preenchida) utilizando a fórmula:
$L_f=L_c+\frac{h_u}{\tan{\alpha}}$
onde L_c é o comprimento do cilindro.

Parte totalmente preenchida

O nível de líquido diretamente na base inferior h₁ pode ser determinado como:
$h_1=h_0+L_f{\tan{\alpha}}$
Se o valor h₁ calculado for maior que o diâmetro do tanque, alguma parte do nosso cilindro está totalmente preenchida com líquido. Então, precisamos calcular o comprimento da parte totalmente preenchida como:
$L_t=\frac{h_1-2{R}}{\tan{\alpha}}$
O cálculo do volume da parte totalmente preenchida é trivial, consulte Cilindro

Após esses cálculos, você pode substituir o comprimento do tanque parcialmente cheio $L=L_f-L_t$ e o nível de líquido h₀ nas fórmulas da primeira seção para calcular o volume da parte parcialmente cheia do tanque inclinado.

PLANETCALC Calculadoras online

Volume de tanque cilíndrico inclinado

Esta página existe graças aos esforços das seguintes pessoas:

Anton

Julia Gomes

Medição de nível do líquido

Volume do líquido em tanque cilíndrico inclinado

Fórmula de volume do tanque inclinado preenchido parcialmente

Determine o comprimento da parte do tanque preenchida com líquido

Parte vazia do tanque

Parte totalmente preenchida

Calculadoras similares

Comentários

PLANETCALC Calculadoras online

Medição de nível do líquido

Volume do líquido em tanque cilíndrico inclinado

Fórmula de volume do tanque inclinado preenchido parcialmente

Determine o comprimento da parte do tanque preenchida com líquido

Parte vazia do tanque

Parte totalmente preenchida

Calculadoras similares

Comentários

Compartilhar nessa página